Алгоритм поиска A-Star с пошаговым описанием кода.

Достижение пункта назначения по наикратчайшему пути – это то, что мы делаем каждый день. A-star (кратко – A*) является одним из наиболее успешных алгоритмов для поиска кратчайшего пути между узлами или графами. Это основанный на имеющейся информации алгоритм поиска, поскольку он использует сведения о стоимости пути и эвристические правила для поиска решения.
В этой статье я сосредоточу внимание на том, как построить алгоритм поиска A-star (a*) с использованием простого кода python. Я обнаружил, что многие статьи или блоги сфокусированы в основном на теории, при этом очень мало информации дается о самой программе. Здесь я попытаюсь пошагово расписать код, максимально просто объяснив детали.
Но для начала немного теории.
А* достигает оптимальности и полноты, двух важных свойств для поисковых алгоритмов.
Когда алгоритм поиска обладает свойством оптимальности, это означает, что он гарантированно найдет наилучшее из возможных решений. Когда алгоритм поиска обладает свойством полноты, это означает, что если решение данной задачи существует, то алгоритм гарантированно найдет его.
Теперь, чтобы понять, как работает A*, для начала нам нужно разобраться со значением некоторых терминов:
- Узел (также называемый Состоянием) – все потенциальные позиции (положения) или остановки с уникальной идентификацией.
- Переход – это акт перемещения между состояниями, или узлами.
- Начальный узел – место, откуда начинается поиск.
- Целевой узел– цель для прекращения поиска.
- Поисковое пространство – это совокупность узлов по аналогии с позициями фигур в настольной игре.
- Стоимость – числовое значение (скажем, расстояние, затраченное время или финансовые затраты) пути от одного узла к другому.
- g (n) - это точная стоимость пути от начального узла до любого узла n
- h (n) — это эвристическая расчетная стоимость от узла n до целевого узла.
- f (n) - наименьшая стоимость в соседнем узле n.
Каждый раз, когда A* входит в узел, он вычисляет стоимость, f(n) (где n – соседний узел), чтобы добраться до всех соседних узлов, а затем входит в узел с наименьшим значением f (n).
Эти значения рассчитываются по следующей формуле:
f(n) = g(n) + h(n)
Здесь мы будем решать проблему лабиринта. Мы должны найти кратчайший путь в лабиринте от начального узла до конечного узла.
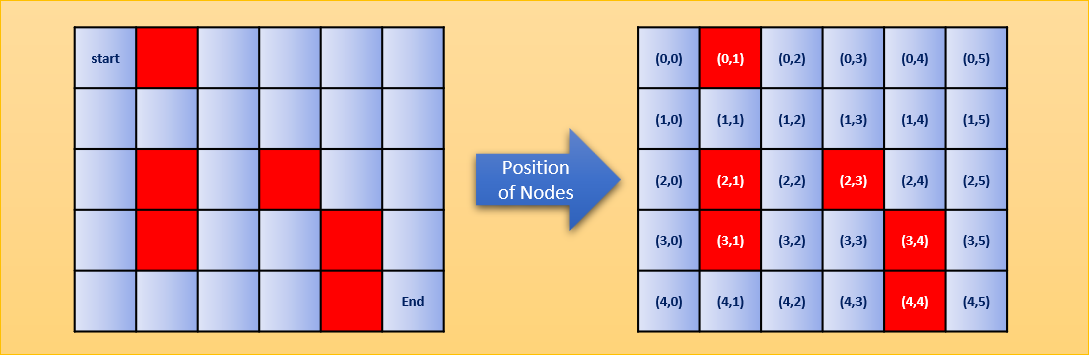
Для этой задачи из лабиринта есть четыре хода (влево, вправо, вверх и вниз) при условии, что допустимый ход доступен. В позициях, обозначенных в виде красного квадрата, движение не допускается (например, в начальной позиции доступно только движение вниз, так как движение вверх и влево заблокировано стеной, а справа – красный квадрат, поэтому движение не допускается).
Я взял код отсюда и из этого блога, который является отличным источником информации.
Итак, сначала мы создадим класс и функцию помощи, приведенные ниже:
(1) класс «узел», который может быть использован для создания объекта для каждого узла с использованием такой информации, как родительский узел, текущее положение в лабиринте и значение стоимости (g, h и f).
(2) нам нужно определить функцию path (путь), которая будет возвращать путь от начального до конечного узла.
Мы определим функцию поиска, которая будет управлять логикой кода:
(3.1 )инициализировать все переменные.
(3.2) добавить начальный узел в «список еще не посещенных объектов». Определите условие остановки во избежание бесконечного повторения цикла. Определите движение с точки зрения относительного положения.
Повторите следующие действия, пока не будут выполнены критерии остановки:
(3.3) найдите квадрат с самой низкой стоимостью f в «списке еще не посещенных объектов». Это будет текущим квадратом. Мы также должны проверить, достигнута или нет максимальная итерация.
(3.4) Проверьте, совпадает ли текущий квадрат с целевым квадратом (это означает, что мы нашли путь).
(3.5) используйте текущий квадрат и проверьте 4 квадрата, соседствующие с этим текущим квадратом, чтобы обновить дочерний узел. Если он не является подвижным или если он находится в «списке еще не посещенных объектов», проигнорируйте его. В противном случае создайте новый узел с помощью родительского узла в качестве текущего узла и обновите положение узла.
(3.7) проверьте все дочерние узлы, созданные для просмотра.
- Если он не находится в «списке еще не посещенных объектов» (кратко – Список), добавьте его в «Список». Сделайте текущий квадрат родительским для этого квадрата. Запишите значения стоимости f, g и h этого квадрата.
- Если он уже находится в «Списке», проверьте, является ли этот путь к этому квадрату лучше, используя в качестве меры стоимость g. Более низкая стоимость g означает, что это лучший путь. Если это так, измените родительский квадрат на текущий квадрат и пересчитайте очки g и f этого квадрата.
(4) Основная программа: мы определим положение лабиринта, начала и конца. Затем мы будем использовать функцию поиска, и если путь существует, мы сможем проложить путь, который будет возвращен по функции path.
Теперь я пошагово пройдусь по коду со ссылкой на шаги, упомянутые выше (см. номер в скобках).
Сначала мы создадим класс для узла, который будет содержать все атрибуты, связанные с узлом, такие как родительский узел, положение узла и все 3 стоимости (g, h и f) для этого узла. Мы инициализируем узел и создаем метод для проверки равенства одного узла относительно другого.

Теперь мы построим функцию path, которая будет использоваться для возврата пути от начального узла к целевому узлу (конечному узлу).
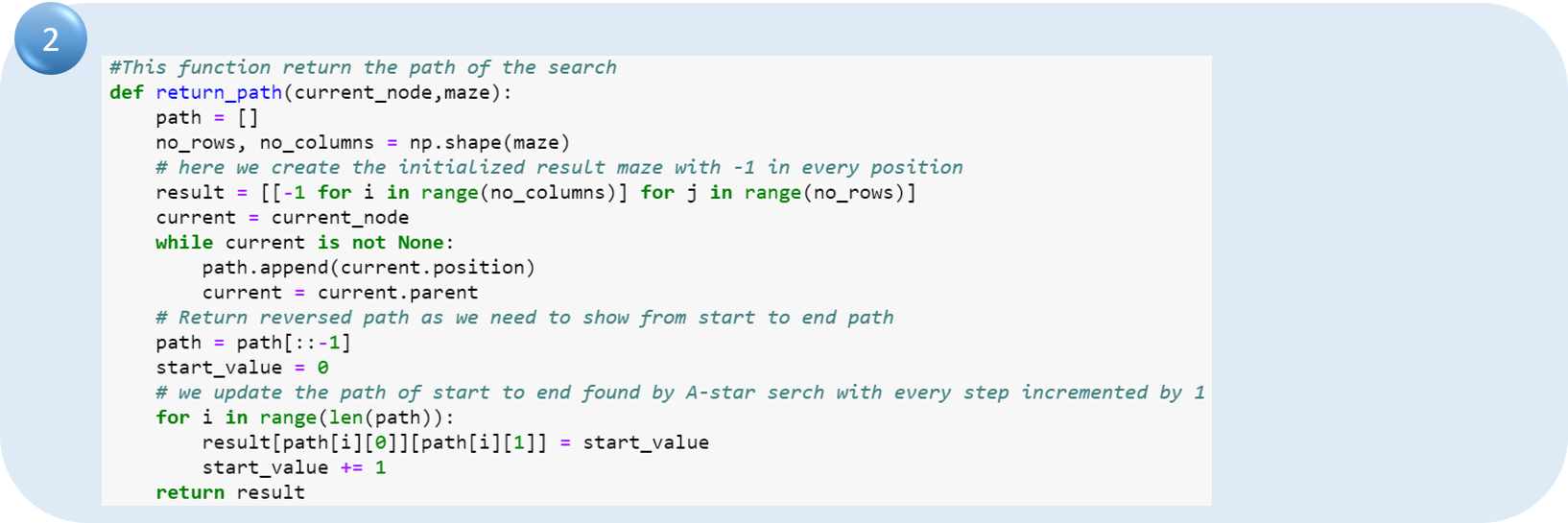
Теперь мы определим функцию поиска, которая имеет несколько шагов. Первым шагом будет инициализация узлов и списков, которые будут использоваться в функции.
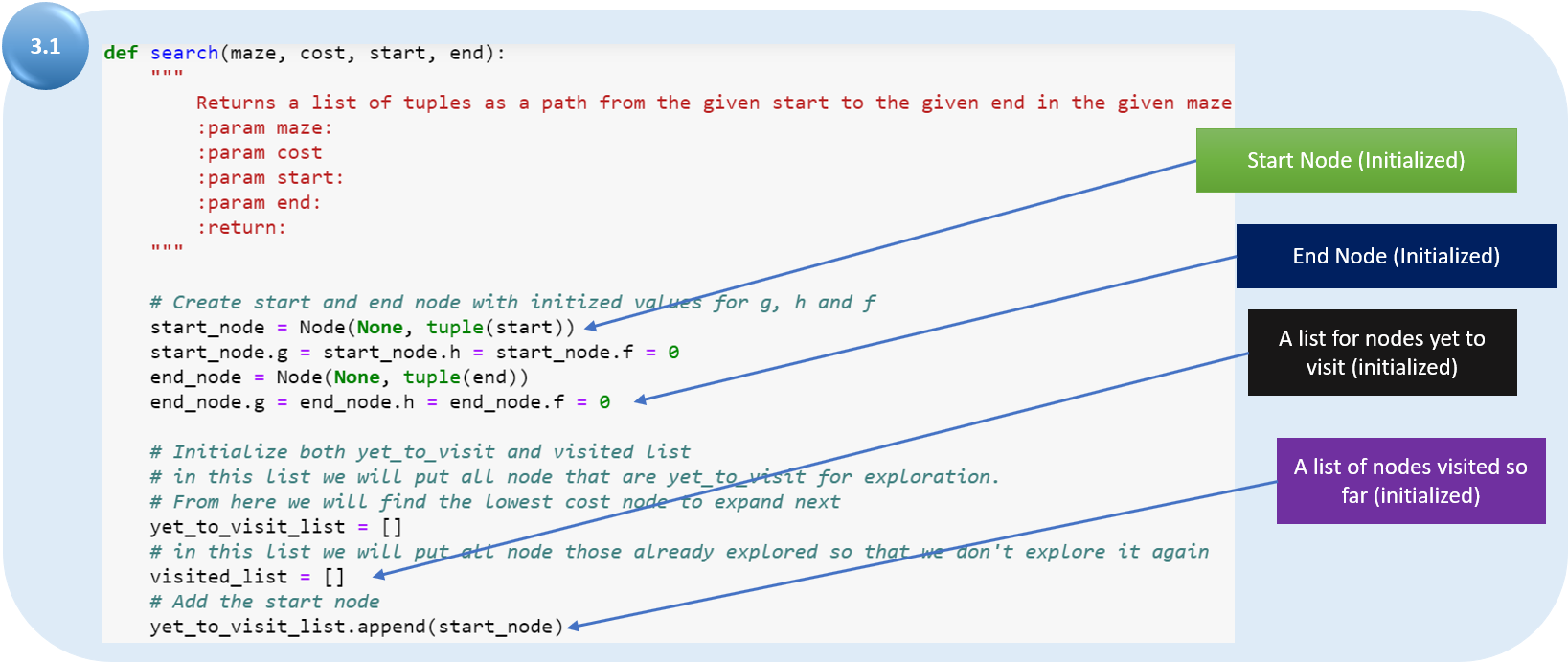
Добавьте начальный узел в «список еще не посещенных объектов». Определите условие остановки, чтобы избежать бесконечного повторения цикла. Определите ход с точки зрения относительного положения, которое будет использоваться для поиска дочернего узла и других относительных положений.
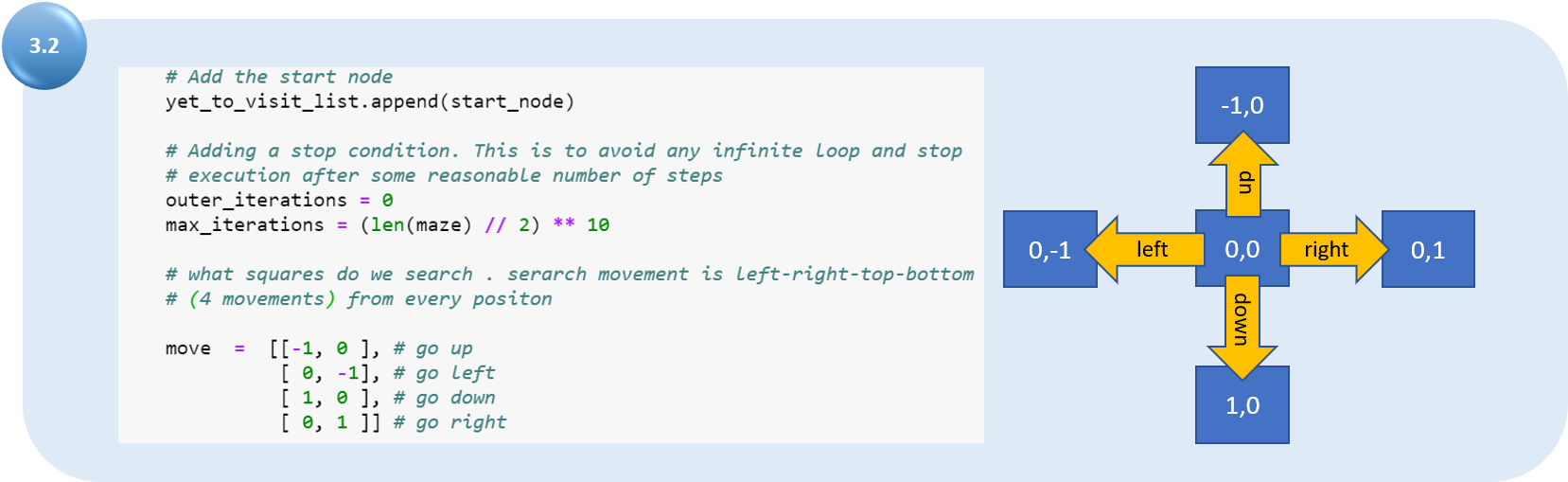
Теперь мы используем текущий узел, сравнивая все затраты f и выбирая самый дешевый узел для дальнейшего расширения. Мы также проверяем, достигнута ли максимальная итерация, устанавливаем сообщение и останавливаем выполнение процесса (избегайте бесконечного повторения цикла).
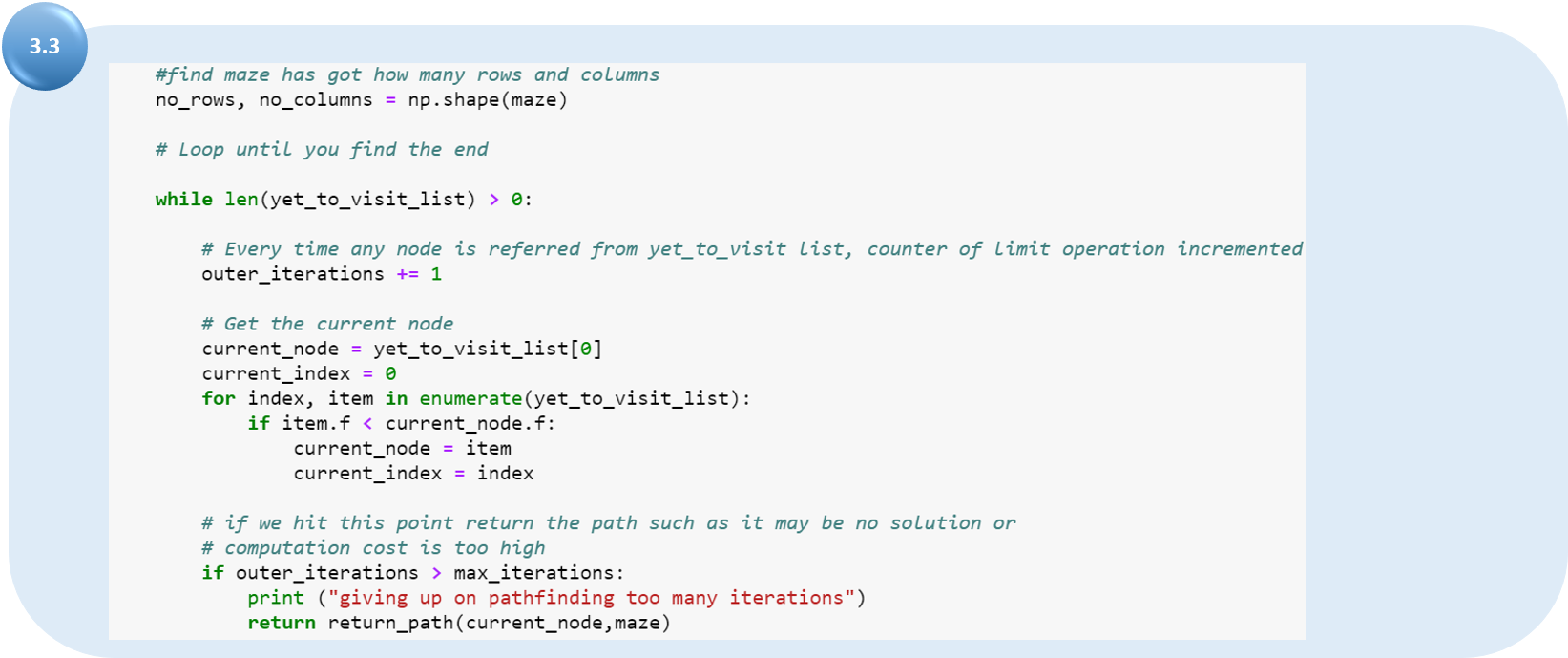
Удалите выбранный узел из «Списка еще не посещенных объектов» и добавьте этот узел в список посещенных. Теперь мы ставим галочку, если целевой квадрат найден. Если целевой квадрат найден, то вызовите функцию path и вернитесь.

Для выбранного узла узнайте все дочерние элементы (используйте ход для поиска дочерних элементов). Получите текущую позицию для выбранного узла (он становится родительским узлом для дочернего):
a) проверьте, существует ли допустимая позиция (пограничная стена сделает несколько узлов недействительными)
b) если какая-либо позиция узла недействительна (Красный квадрат), то проигнорируйте ее
c) добавьте в список допустимых дочерние узлы для выбранного родительского узла
Здесь на схеме мы показываем, что узел с черным кругом внутри является текущим узлом, а узлы с зеленым кругом являются допустимыми дочерними узлами.
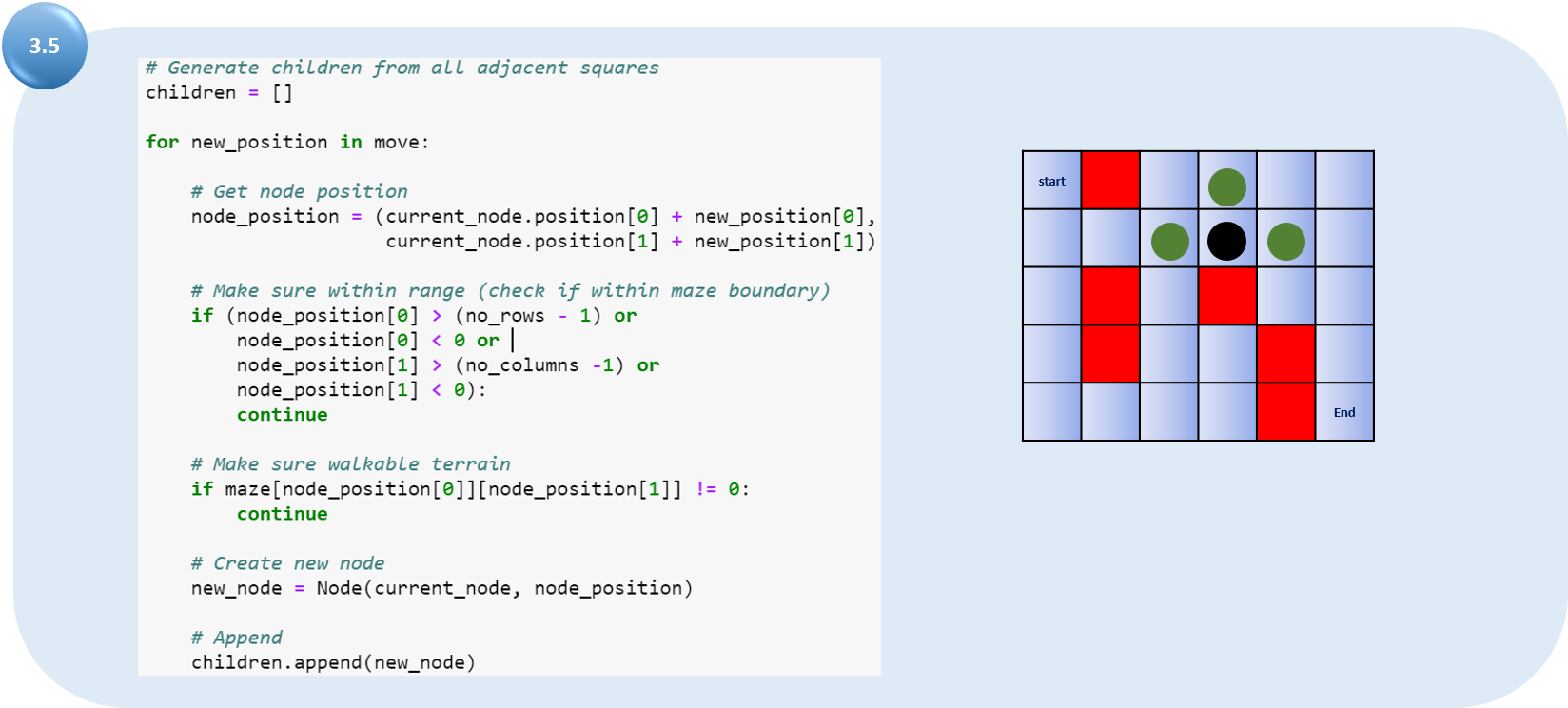
Для всех дочерних узлов:
a) если дочерний узел находится в списке посещенных, тогда пропустите его и попробуйте следующий дочерний узел;
b) вычислите значения g, h и f для дочернего узла. Для h эвристика стоимости достижения целевого узла для текущего узла рассчитывается здесь с использованием евклидова расстояния;
c) если дочерний узел в «Списке еще не посещенных объектов», то проигнорируйте его или переместите в «Список еще не посещенных объектов».
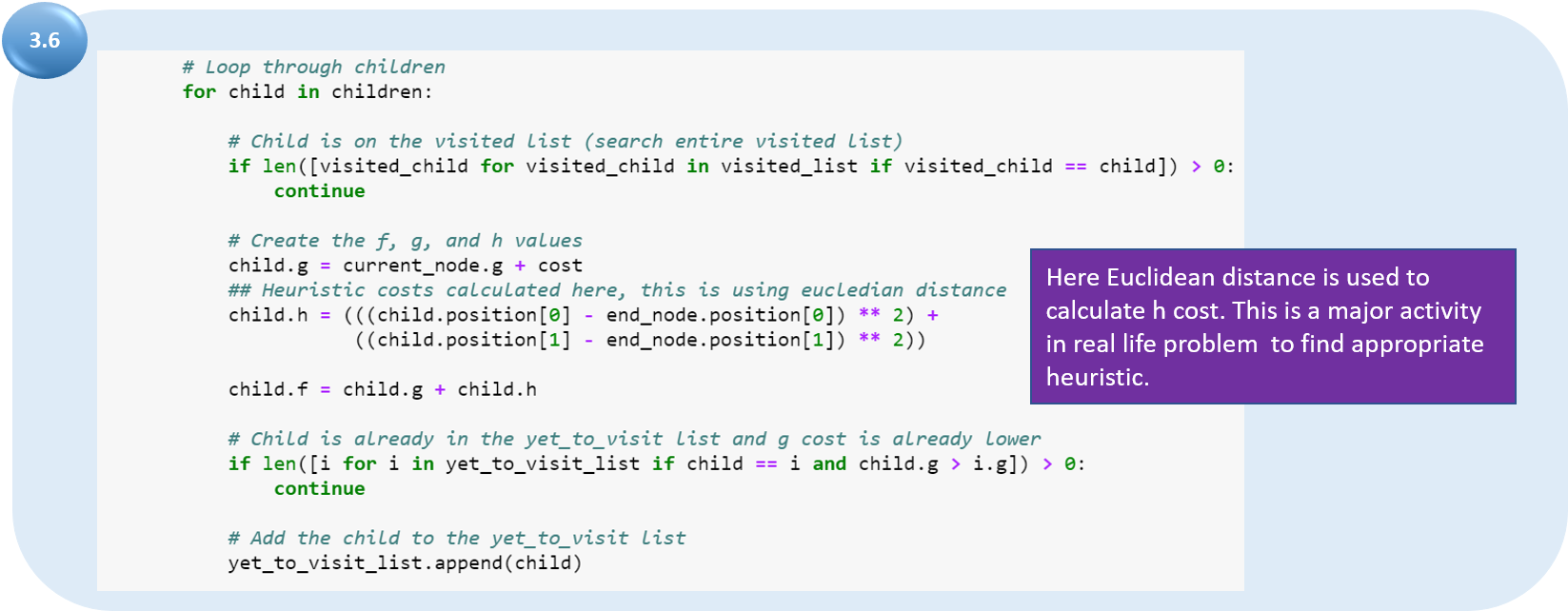
Теперь, наконец, мы запустим программу из основной сети (main) с лабиринтом и получим путь. См. путь, также показанный с помощью стрелки.
Вывод
A-star (A*) – это очень мощный алгоритм в области искусственного интеллекта с широким диапазоном использования. Однако его польза ограничивается его эвристической функцией (которая может быть очень изменчивой, учитывая природу проблемы). A* - это самое популярное решение для поиска пути, потому что этот алгоритм довольно гибкий.
Он нашел применение во многих программных системах, от машинного обучения и поисковой оптимизации до разработки игр, где персонажи перемещаются по сложной местности и препятствиям, чтобы добраться до игрока.
Вы можете найти полный код на Github.
Комментарии:
Не понял
#
Зачем это здесь?
ср, 01/15/2020 - 15:40